Mathematics is building block of Machine learning. I know math is hard to understand but it is much needed as well. Singular value decomposition (SVD) is one mathematical method used in various applications.
Singular Value Decomposition is a matrix factorization method which is used in various domains of science and technology. Furthermore, due to recent great developments of machine learning, data mining and theoretical computer science, SVD has been found to be more and more important. It is not only a powerful tool and theory but also an art.
Singular value decomposition makes matrices become a “Language” of data science.
**Matrix Factorization: **It** **is a representation of a matrix into a product of matrices. There are many different matrix factorization and each used for different class of problems.
Mathematics behind SVD
For a m × n matrix(M) there exists a singular value decomposition of **M, **of the form
where
-
U is a *m × m *unitary matrix. (left singular vector)
-
Σ is a m × *n *diagonal matrix with non-negative real numbers.
-
V is a n × *n *unitary matrix* *. ( right singular vector)
-
V* is the conjugate transpose of the n × n unitary matrix.
-
The diagonal values of Σ are known as Singular values of** M**.
**Conjugate Transpose: **The conjugate transpose of a matrix interchanges the row and column index for each element.
Identity matrix: It is a square matrix in which all the elements of the principal diagonal are ones and all other elements are zeros.
**Diagonal Matrix: **It** **is a matrix in which the entries outside the main diagonal are all zero.
**Unitary matrix: **Matrices whose conjugate transpose is also its inverse, that is UU*=I.
**Singular Values: **Basically it denotes the square root of the eigenvalues of XX* where X is a matrix.
Intuition
-
Consider any 2 independent vectors lying in a plane both starting at the origin. Rotate the vectors by an arbitrary angle and importantly such that the vector with the larger x value has a lower absolute y value than the other. The 2 points will lie on the boundary of an ellipse centered on the origin.
-
Scale the ellipse(2 vectors) to a unit circle and inspect the angle between the two unit vectors.
-
Vary the angle of the rotation and repeat the scaling until the scaled unit vectors are orthogonal.
-
Finally rotate the unit vectors by angle β until they correspond to x-axis and y-axis.
The above process describes is the inverse of SVD.
The expression UΣV* can be interpreted as a composition of three geometrical transformations: a rotation, a scaling, and another rotation. SVD is generally used for data compression in various fields. Other than data compression the resultant matrices has lots of wonderful properties.
if M is symmetric positive definite its eigenvectors are orthogonal and we can write M= QΣQ*. This is a special case of a SVD, with U = V = Q
For mathematical example, refer to this link.
Principal Component Analysis
Principal components analysis is a procedure for identifying a smaller number of uncorrelated variables, called “principal components”, from a large set of data. The goal of principal components analysis is to explain the maximum amount of variance with the fewest number of principal components. For more details, go through this blog.
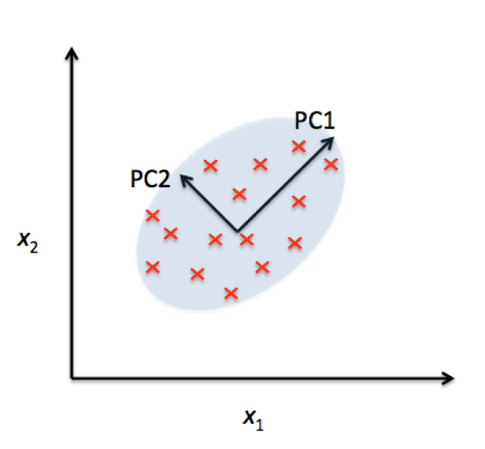
Relation between PCA and SVD-
Let M be m × n matrix where m is the number of samples and n is the number of features
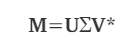
The covariance matrix of M is C
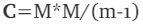
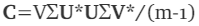
Note : The above is correct only if M is centered(scaled). Only then is covariance matrix equal to M*M/(m−1). That is why we need to center the intial dataset M for PCA.
The right singular vectors V are principal directions and Principal components are given by MV=UΣV*V=UΣ. To reduce the dimensionality of the data from m to k where k<m, select the first k columns of UΣ.
Other Applications
References
Footnotes
This blog tries to aware you about the basic mathematics of singular value decomposition and different application of singular value decomposition. Go through the references to understand it thoroughly.
❤ if this was good read.
P.S. — Suggestions would be highly appreciated.